O (N 对数 N)复杂度-类似于线性？

所以我想我会因为问了这样一个琐碎的问题而被埋葬，但是我对一些事情有点困惑。

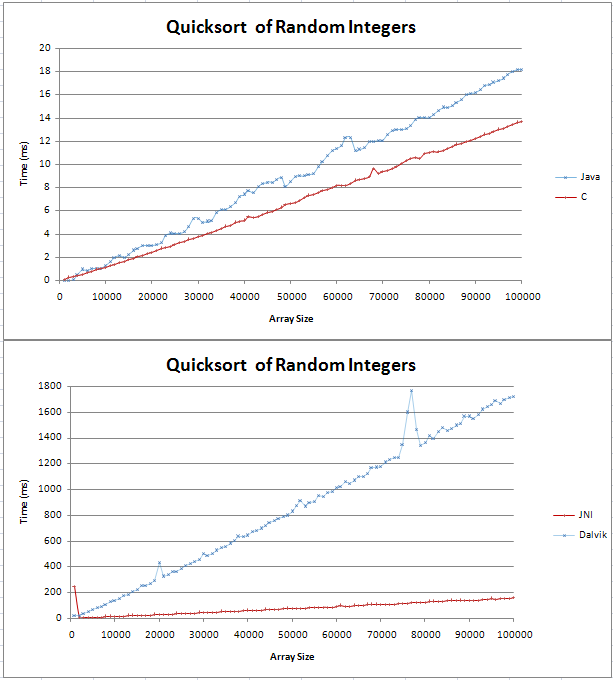
我用 Java 和 C 实现了快速排序，并且做了一些基本的比较。图表显示为两条直线，C 比 Java 快4毫秒，超过100,000个随机整数。

Results

我的测试代码可以在这里找到;

机器人-基准

我不确定(n log n)线会是什么样子，但我认为它不会是直的。我只是想检查这是否是预期的结果，并且不应该尝试在代码中查找错误。

我把公式输入 Excel，对于基数10，它似乎是一条直线，在开始时有一个扭结。这是因为 log (n)和 log (n + 1)之间的差值是线性增加的吗？

谢谢,

盖文

106260 次浏览
小开
最佳答案

Make the graph bigger and you'll see that O(n logn) isn't quite a straight line. But yes, it is pretty near to linear behaviour. To see why, just take the logarithm of a few very large numbers.

For example (base 10):

log(1000000) = 6
log(1000000000) = 9
…

So, to sort 1,000,000 numbers, an O(n logn) sorting adds a measly factor 6 (or just a bit more since most sorting algorithms will depend on base 2 logarithms). Not an awful lot.

In fact, this log factor is so extraordinarily small that for most orders of magnitude, established O(n logn) algorithms outperform linear time algorithms. A prominent example is the creation of a suffix array data structure.

A simple case has recently bitten me when I tried to improve a quicksort sorting of short strings by employing radix sort. Turns out, for short strings, this (linear time) radix sort was faster than quicksort, but there was a tipping point for still relatively short strings, since radix sort crucially depends on the length of the strings you sort.

小开

log(N) is (very) roughly the number of digits in N. So, for the most part, there is little difference between log(n) and log(n+1)

小开

Try plotting an actual linear line on top of it and you'll see the small increase. Note that the Y value at 50,0000 is less than the 1/2 Y value at 100,000.

It's there, but it's small. Which is why O(nlog(n)) is so good!

小开
  1. Usually the O( n*log(n) ) algorithms have a 2-base logarithmic implementation.
  2. For n = 1024, log(1024) = 10, so n*log(n) = 1024*10 = 10240 calculations, an increase by an order of magnitude.

So, O(n*log(n)) is similar to linear only for a small amount of data.

Tip: don't forget that quicksort behaves very well on random data and that it's not an O(n*log(n)) algorithm.

小开

For even more fun in a similar vein, try plotting the time taken by n operations on the standard disjoint set data structure. It has been shown to be asymptotically n α(n) where α(n) is the inverse of the Ackermann function (though your usual algorithms textbook will probably only show a bound of n log log n or possibly n log* n). For any kind of number that you will be likely to encounter as the input size, α(n) ≤ 5 (and indeed log* n ≤ 5), although it does approach infinity asymptotically.

What I suppose you can learn from this is that while asymptotic complexity is a very useful tool for thinking about algorithms, it is not quite the same thing as practical efficiency.

小开

FYI, quicksort is actually O(n^2), but with an average case of O(nlogn)

FYI, there is a pretty big difference between O(n) and O(nlogn). That's why it's not boundable by O(n) for any constant.

For a graphical demonstration see:

O(n) vs O(nlogn)

小开

Any data can be plotted on a line if the axes are chosen correctly :-)

Wikipedia says Big-O is the worst case (i.e. f(x) is O(N) means f(x) is "bounded above" by N) https://en.wikipedia.org/wiki/Big_O_notation

Here is a nice set of graphs depicting the differences between various common functions: http://science.slc.edu/~jmarshall/courses/2002/spring/cs50/BigO/

The derivative of log(x) is 1/x. This is how quickly log(x) increases as x increases. It is not linear, though it may look like a straight line because it bends so slowly. When thinking of O(log(n)), I think of it as O(N^0+), i.e. the smallest power of N that is not a constant, since any positive constant power of N will overtake it eventually. It's not 100% accurate, so professors will get mad at you if you explain it that way.

The difference between logs of two different bases is a constant multiplier. Look up the formula for converting logs between two bases: (under "change of base" here: https://en.wikipedia.org/wiki/Logarithm) The trick is to treat k and b as constants.

In practice, there are normally going to be some hiccups in any data you plot. There will be differences in things outside your program (something swapping into the cpu ahead of your program, cache misses, etc). It takes many runs to get reliable data. Constants are the biggest enemy of trying to apply Big O notation to actual runtime. An O(N) algorithm with a high constant can be slower than an O(N^2) algorithm for small enough N.


提交答案