最佳答案
如何在广度优先搜索中追踪路径?
如何追踪广度优先搜索的路径,例如:
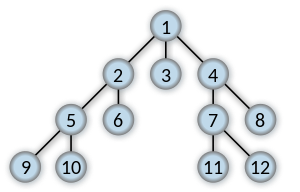
如果搜索键 11,返回连接1到11的 最短的列表。
[1, 4, 7, 11]
如何追踪广度优先搜索的路径,例如:

如果搜索键 11,返回连接1到11的 最短的列表。
[1, 4, 7, 11]